জ্যামিতি কাকে বলে?
জ্যা অর্থ ভূমি আর মিতি অর্থ পরিমাপ। অতএব, জ্যামিতি শাস্ত্রের আভিধানিক অর্থ হল ভূমির পরিমাপ বা জরিপ। গণিতবিদ্যার যে শাখায় ভূমি বা স্থানের পরিমাপ সম্পর্কে বিশদ আলােচনা করা হয়, তাকে জ্যামিতি বলে। জ্যামিতির ইংরেজি প্রতিশব্দ হলাে Geometry। Geo মানে পৃথিবী এবং metry মানে measurment অর্থাৎ পরিমাপ। শব্দটি গ্রিক শব্দ হতে উৎপন্ন। এটি গ্রিক শব্দ ‘জ্যা’ ও ‘মিতি’ নিয়ে গঠিত।
জ্যামিতিকে স্থানভিত্তিক বিজ্ঞানও বলা হয়। আধুনিক গণিতবিদদের মতে, বিভিন্ন প্রকার চিহ্ন ও তাদের ধর্ম বা বৈশিষ্ট্যের বিচার বিশ্লেষণকেই মূলত জ্যামিতি বলে।
জ্যামিতি কত প্রকার
ব্যবহার ভেদে জ্যামিতিকে দুইভাগে ভাগ করা যায়। যথা : ব্যবহারিক জ্যামিতি ও তাত্ত্বিক জ্যামিতি।
1. ব্যবহারিক জ্যামিতি : জ্যামিতি শস্ত্রের যে শাখা পাঠ করলে বিন্দু, বস্তু, স্থান, রেখা, কোণ, ক্ষেত্র, তল প্রভৃতি অঙ্কন করার পদ্ধতি হাতে কলমে শেখা যায়তাকে ব্যবহারিক জ্যামিতি বলে।
2. তাত্ত্বিক জ্যামিতি : জ্যামিতি শাস্ত্রের যে শাখা পাঠ করলে জ্যামিতিক উপাত্তগুলােকে সত্য বলে প্রমাণ করা যায় এবং তা থেকে যুক্তি তর্ক ও তত্ত্বের সাহায্যে নতুন কোন সিদ্ধান্তে আসা যায় তাকে তাত্ত্বিক জ্যামিতি বলে।
এছাড়া জ্যমিতিকে আরো দুইভাগে ভাগ করা যায়। যথা: তল জ্যামিতি এবং ঘন জ্যামিতি।
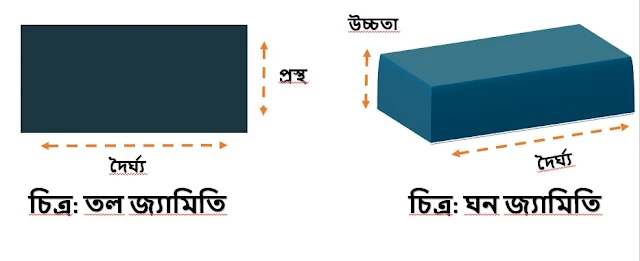
3. তল জ্যামিতি : তল জ্যামিতি দুমাত্রার। অর্থাৎ দৈর্ঘ্য ও প্রস্থ (লম্বা ও চওড়ার) বিষয়টি আলােচিত হয়ে থাকে।
তল দুই প্রকার : সমতল ও বক্রতল।
- সমতল : যে কোন দুটি বিন্দুর সংযােজকে সরলরেখা যদি তলের উপরে অবস্থিত থাকে তাকে সমতল বলে। যেমন : চেয়ার, টেবিল, বই।
- বক্রতল/অসমতল : যে তলের পৃষ্ঠ বা উপরিভাগ সমান নয় তাকে বক্রতল বা অসমতল বলে। যেমন : মার্বেল, বল, কমলা ইত্যাদি।
জ্যামিতির বিভিন্ন অংশ
স্থান : কোন বস্তু যতটুকু জায়গা দখল করে সেই জায়গাকে স্থান বলে। যেমন বাক্স, টেবিল, চেয়ার ইত্যাদি।
বস্তু : যে বস্তু জায়গা দখল করে তাকেই বস্তু বলে। যেমন : বই, খাতা, টেবল। বস্তুর মাত্রা হল তিনটি। যথা : দৈর্ঘ্য, প্রস্থ, এবং উচ্চতা। বস্তুর মাত্রার উপর ভিত্তি করে বস্তুকে তিনভাগে ভাগ করা হয়েছে। যথা : একমাত্রিক, দ্বিমাত্রিক ও ত্রিমাত্রিক।
- একমাত্রিক: যে বস্তুর একটি মাত্রা আছে, তাকে বলে একমাত্রিক। যেমন : রেখা দৈর্ঘ্য।
- দ্বিমাত্রিক : যে বস্তুর দুইটি মাত্রা আছে, তাকে বলে দ্বিমাত্রিক। যেমন : তল (দৈর্ঘ্য ও প্রস্থ)
- ত্রিমাত্রিক : যে বস্তুর তিনটি মাত্রা আছে, তাকে বলে ত্রিমাত্রিক। যেমন : ঘনবস্তু। ঘনবস্তুর তিনটি মাত্রা থাকে। যথা (দৈর্ঘ্য, প্রস্থ ও উচ্চতা)।
বিন্দু : দুইটি রেখা পরস্পরকে ছেদ করলে তখন বিন্দুর উপত্তি হয়। বিন্দুর শুধু অবস্থান আছে কিন্তু কোন মাত্রা নেই। বিভিন্ন প্রকার বিন্দু এবং তার অবস্থান। যথা:
- সমরেখ বিন্দু : যেসব বিন্দু একই সরলরেখায় অবস্থান করে তাদেরকে সমরেখ বিন্দু বলে।
- সমবিন্দুরেখ : দুই বা ততােধিক সরলরেখার একটি সাধারণ বিন্দু থাকলে তবে উক্ত
- রেখাগুলােকে ঐ বিন্দুর সমবিন্দুরেখ বলে।
- সমতলবিন্দু : যে সকল বিন্দু একই তলের উপর অবস্থান করে তাকে সমতলবিন্দু বলে।
- শীর্ষবিন্দু : দুটি বাহু যখন কোন একটি সাধারণ বিন্দুতে মিলিত হয় তখন তাকে শীর্ষ
- বিন্দু বলে।
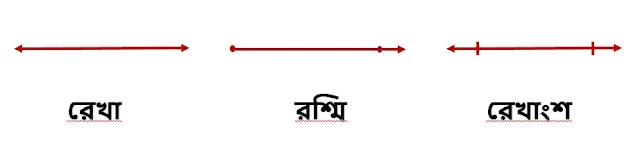
রেখা : চলন্ত-বিন্দুর গতিপথকে রেখা বলে। সুতরাং বিন্দুর চলার পথকে রেখা বলে। রেখার দৈর্ঘ্য আছে, কিন্তু প্রস্থ ও উচ্চতা বা বেধ নেই।
রেখা।
রশ্মি : যার নির্দিষ্ট দৈর্ঘ্য নেই, কিন্তু প্রান্তবিন্দ আছে তাকে রশ্মি বলে।
রেখাংশ : যার নির্দিষ্ট দৈর্ঘ্য আছে, কিন্তু ১টি প্রান্তবিন্দু আছে, তাকে রেখাংশ বলে।
রেখা সাধারণত দুই প্রকার
১. সরলরেখা ও
২. বক্ররেখা।
সরলরেখা : যে রেখা এক বিন্দু থেকে অন্য বিন্দুতে বা এক অবস্থান থেকে অন্য অবস্থানে পৌছতে দিক পরিবর্তন করে না তাকে সরলরেখা বলে।
বক্ররেখা : যে রেখা এক বিন্দু থেকে অন্য বিন্দুতে বা এক অবস্থান থেকে অন্য অবস্থানে পৌছতে দিক পরিবর্তন করে তাকে বক্ররেখা বলে।
সমান্তরাল রেখা : দুটি রেখা যদি পরস্পরের মধ্যে সর্বদা সমান দূরত্ব বজায় রেখে চলতে থাকে তবে তাকে সমান্তরাল রেখা বলে।

একটি মন্তব্য পোস্ট করুন
Do not enter any harmful link