কোণ কাকে বলে? কোণের প্রকারভেদ

কোণ কাকে বলে?

দুইটি সরলরেখা কোন একটি বিন্দুতে মিলিত হলে ঐ মিলিত স্থানে একটি কোন উৎপন্ন হয়। 

লক্ষ করি ?

১। যে বিন্দুতে কোণ উৎপন্ন হয় ঐ বিন্দুকে মাঝখানে রাখতে হয়।

২। যে দুটি রেখা দ্বারা কোণ উৎপন্ন হয় তাদেরকে কোণের বাহু বা ভূজ বলে।

৩। বাহু দুটির মিলন বিন্দুকে কৌনিক বিন্দু বলে। 

কোণের পরিমাণ: কোণ পরিমাপের একক হল ডিগ্রী। এক সমকোণের পরিমাণ 90°। দুই সমকোণের পরিমাণ 180°। সরলকোণের 180 ভাগের প্রত্যেক ভাগকে 1° বলা হয়। কোণ পরিমাণের জন্য চাদা ব্যবহার করা হয়।

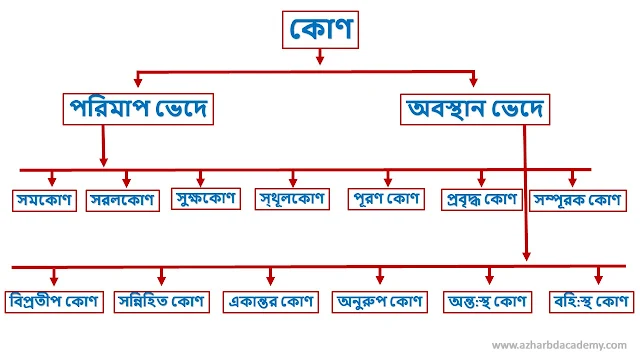
কোণ কত প্রকার ও কি কি

কোণ পরিমাপভেদে ও অবস্থানভেদে এই দুভাগে বিভক্ত। 

১. পরিমাপভেদে : সমকোণ, সরলকোণ, সূক্ষকোণ, স্থূলকোণ, প্ৰবৃদ্ধকোণ, পূরক কোণ,  সম্পূরক কোণ। এবং

২. অবস্থানভেদে: বিপ্রতীপ কোণ, সন্নিহিত কোণ, একান্তর কোণ, অনুরুপ কোণ,  অন্তঃস্থ কোণ, বহিঃস্থ কোণ, শিরঃ কোণ, উন্নতিকোণ, অবনতি কোণ, কেন্দ্রস্থ কোণ, বৃত্তস্থ কোণ,  অর্থবৃত্ত কোণ, রৈখিক যুগল কোণ।

পরিমাপভেদে কোণসমূহ

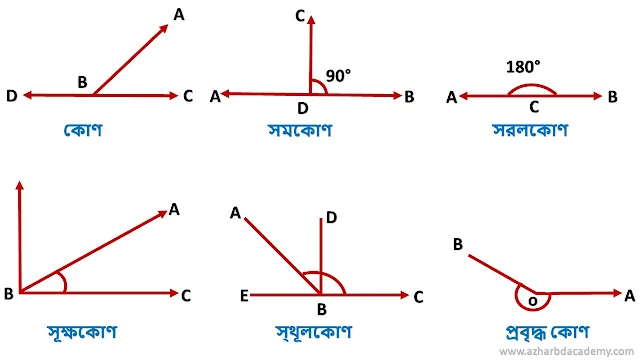
১. সমকোণ : একটি সরলরেখার উপর আরেকটি সরলরেখা লম্বভাবে দণ্ডায়মান হলে যে দুইটি সন্নিহিত কোণ উৎপন্ন। তাদের প্রত্যেকটিকে সমকোণ বলা হয়। চিত্রে AB সরলরেখার উপর CD লম্ব। কাজেই সন্নিহিত ∠ADC = সন্নিহিত ∠BDC = 1 সমকোণ।

২. সরলকোণ : দুই সমকোণের সম-পরিমাণ কোণকে সরুল কোণ বলা হয়। চিত্রে ∠ACB হল একটি সরল কোণ। এক সরলকোণ = 180°।

আরো পড়ুন, চতুর্ভুজ এর বৈশিষ্ট্য ও প্রকারভেদ

৩. সূক্ষ্মকোণ : এক সমকোণের চেয়ে ছােট কোণকে সূক্ষ্মকোণ বলা হয়। চিত্রে ∠ABC এক সমকোণের চেয়ে ছােট। তাই ∠ABC একটি সূক্ষ্মকোণ

৪. স্থূলকোণ : এক সমকোণের চেয়ে বড় কিন্তু দুই সমকোণের চেয়ে ছােট কোণকে স্থলকোণ বলা হয়। চিত্রে ∠ABC, এক সমকোণ∠DBC এর চেয়ে বড় কিন্তু দুই সমকোণ ∠EBC এর চেয়ে ছােট। তাই ∠ABC একটি স্থূলকোণ।

৫. প্রবৃদ্ধ কোণ : দুই সমকোণ অপেক্ষা বড় কিন্তু চার সমকোণ অপেক্ষা ছােট কোণকে প্রবৃদ্ধ কোণ বলা হয়। ব্যাখ্যা : চিত্রে, ∠AOB একটি প্রবৃদ্ধ কোণ।

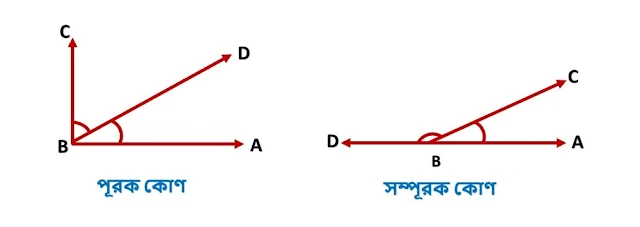
৬. পূরক কোন : দুইটি সন্নিহিত কোণের সমষ্টি এক সমকোণের সমান হলে ঐ দুটি কোণের একটিকে অপরটির পূরক কোণ বলা হয়। ব্যাখ্যা : চিত্রে, সন্নিহিত ∠ABD + সন্নিহিত  ∠CBD = ∠ABC = 1 সমকোণ। তাই ∠ABD কোণ হল ∠CBD-এর পূরক কোণ। অথবা ∠CBD হল  ∠ABD-এর পূরক কোণ।

৭. সম্পূরক কোণ : দুইটি সন্নিহিত কোণের সমষ্টি দুই সমকোণের সমান হলে, একটি কোণকে অপরটির সম্পূরক কোণ বলা হয়। চিত্রে সন্নিহিত ∠ABC + সন্নিহিত ∠CBD দুই সমকোণ। তাই ∠ABC হল ∠CBD-এর সম্পূরক কোণ অথবা, ∠CBD হল ∠ABC-এর সম্পূরক কোণ।

আরো পড়ুন, ত্রিভূজের বৈশিষ্ট্য ও প্রকারভেদ

অবস্থানভেদে কোণসমূহ

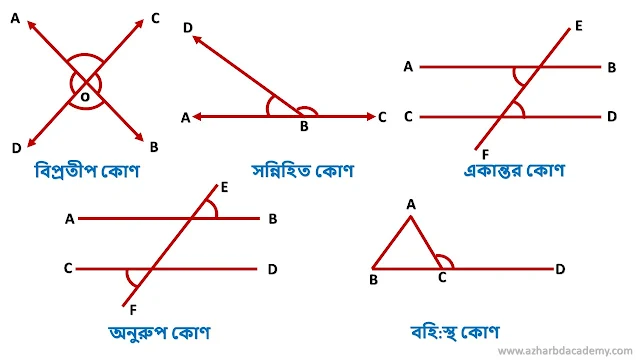
১. বিপ্রতীপ কোণ : দুইটি কোণের একই শীর্ষ বিন্দু হলে এবং একটি কোণের বাহুদ্বয় অপর কোণের বাহুদ্বয়ের বিপরীত রশ্মি হলে, কোণ দুইটিকে পরস্পরের বিপ্রতীপ কোণ বলা হয়। চিত্রে ∠AOD ও ∠COB পরস্পর বিপ্রতীপ কোণ। অপর দিকে ∠AOC ও ∠DOB পরস্পর বিপ্রতীপ কোণ। বৈশিষ্ট্য : বিপ্রতীপ কোণদ্বয় পরস্পর সমান। ∠AOD বিপ্রতীপ ∠COB এবং ∠AOC = বিপ্রতীপ ∠DOB।

২. সন্নিহিত কোণ : দুইটি কোণের একই শীর্ষ বিন্দু এবং একটি সাধারণ বাহু থাকলে কোণ দুইটিকে সন্নিহিত কোণ বলা হয়। চিত্রে ∠ABD ও ∠CBD হল সন্নিহিত কোণ।

৩. একান্তর কোণঃ দুইটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা ছেদ করলে ছেদের বিপরীত পাশে সমান্তরাল যে রেখা-কোণ উৎপন্ন করে তাকে একান্তর কোণ বলে।

৪. অনুরূপ কোণ: দুইটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা ছেদ করলে ছেদকের একই পার্শ্বে যে কোণ উৎপন্ন হয় তাকে বলে অনুরূপ কোণ।

৫. অন্তস্থ কোণ: কোণ তলের অভ্যন্তরে বাহু গুলাে যে কোণ উৎপন্ন করে তাকে অন্তস্থ কোণ বলে। কোণ সরলরেখার দুটি বিন্দুতে মিলিত হলে সেখানে যে কোণ উৎপন্ন হয় তাকে অন্ত:স্থকোণ বলে।

৬. বহিঃস্থ কোণ : যে কোন ত্রিভুজের একটি বাহুকে বর্ধিত করলে ত্রিভুজের বাইরে যে  কোণ উৎপন্ন হয় তাকে বহিঃস্থ কোণ বলা হয়। চিত্রে ∠ABC-এর BC বাহুকে D পর্যন্ত বর্ধিত করায় ত্রিভুজের বাইরে ∠ACD উৎপন্ন হয়েছে। তাই ∠ACD, ত্রিভুজ ABC এর বহিঃস্থ কোণ।

৭. রৈখিকযুগল কোণ:  ও দুটি সন্নিহিত কোণের বহি:স্থ বাহুদ্বয় যদি বিপরীত রশ্মি হয়  অর্থাৎ একই সরল রেখার অংশ হয়, তবে কোণ দুটিকে রৈখিক  ‍যুগল কোণ বলা হয়।